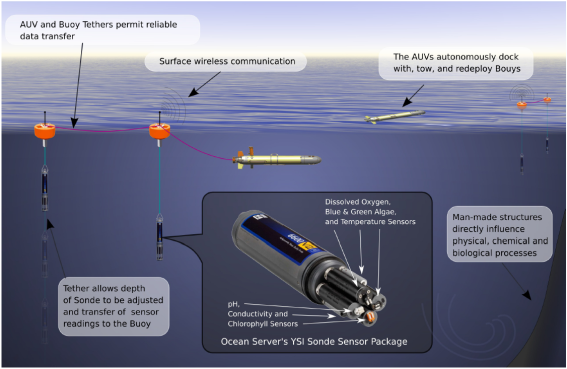
This project, in collaboration with Texas AM and ASU, studies modeling, planning, and control for adaptive sampling using underwater and/or surface vehicles. The primary application is environmental monitoring of water quality.

This work develops agile pick-and-place capabilities using a VTOL aerial vehicles such as quadrotors. The goal is to achieve predictable, reliable, and efficient object manipulation. This is achieved by identifying accurate systems models and employing optimal trajectory generation exploiting the multi-body dynamics of the system.

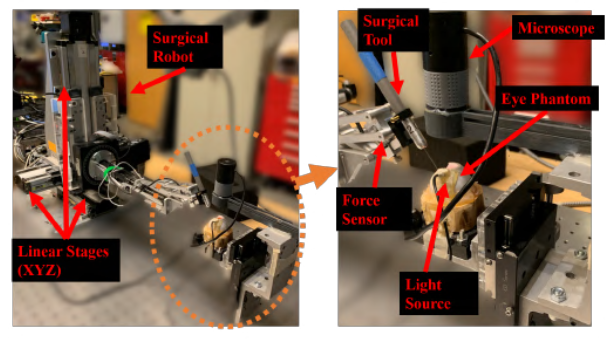
This work develops control and motion planning algorithms for safe and autonomous robot-assisted eye surgery.

This work develops planning and control algorithms for autonomous navigation of ground vehicle on rough terrains. The approach is based on global stochastic optimization and local optimal control of trajectories simulated using high-fidelity physics engine. The system is currently being deployed on a small-scale ground vehicle at JHU.

This work considers motion planning for small satellites such as cubesats performing proximity operations in a several meters range of a target object. The main goal is to develop a principled methodology for handling the coupled effects of orbital dynamics, rotational and translational rigid body dynamics, underactuation and control bounds, obstacle avoidance, and sensor field-of-view constraints. Simulated examples are developed to illustrate the approach. In addition, a 2-D experimental testbed consisting of an air-bearing table and cubesat engineering models is developed for partial testing and integration of the proposed methods.

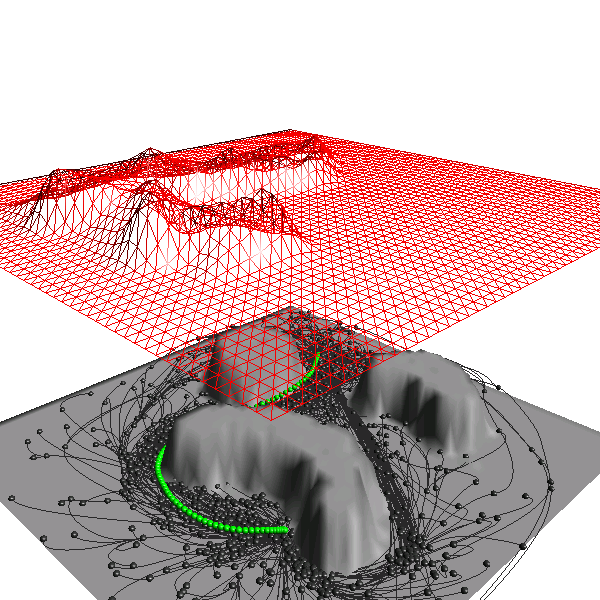
This work is concerned with motion planning for nonlinear robotic systems operating in constrained environments. A method for computing high-quality trajectories is proposed building upon recent developments in sampling-based motion planning and stochastic optimization. The idea is to equip sampling-based methods with a probabilistic model that serves as a sampling distribution and to incrementally update the model during planning using data collected by the algorithm. At the core of the approach lies the cross-entropy method for estimation of rare-event probabilities. The cross-entropy method is combined with rapidly-exploring random tree methods in order to handle complex environments. The main goal is to provide a framework for consistent adaptive sampling that correlates the spatial structure of trajectories and their computed costs. Exploiting this structure then results in marked increase in performance.

This work considers a hybrid Visual Servoing technique for differentially flat underactuated systems. Given a goal image, the objective is to navigate to a position which aligns the camera with the desired image while keeping salient features in view along the way. We formulate the problem as an optimal control problem that can be solved using Gauss-Newton optimization. As a cost function, we use the average squared distance between SURF features matched between the desired image and the image projected from the final state of the trajectory. The optimization is performed over a polynomial parametrization of the flat outputs of the system to decrease the dimensionality of the optimization. Preliminary experimental results show that the technique has better performance compared to a typical position-based visual servoing system for the case considered, which is a simulated quadrotor with a front-facing camera. This method assumes feature depths are known or can be estimated (e.g. using stereo camera or structure from motion algorithms).

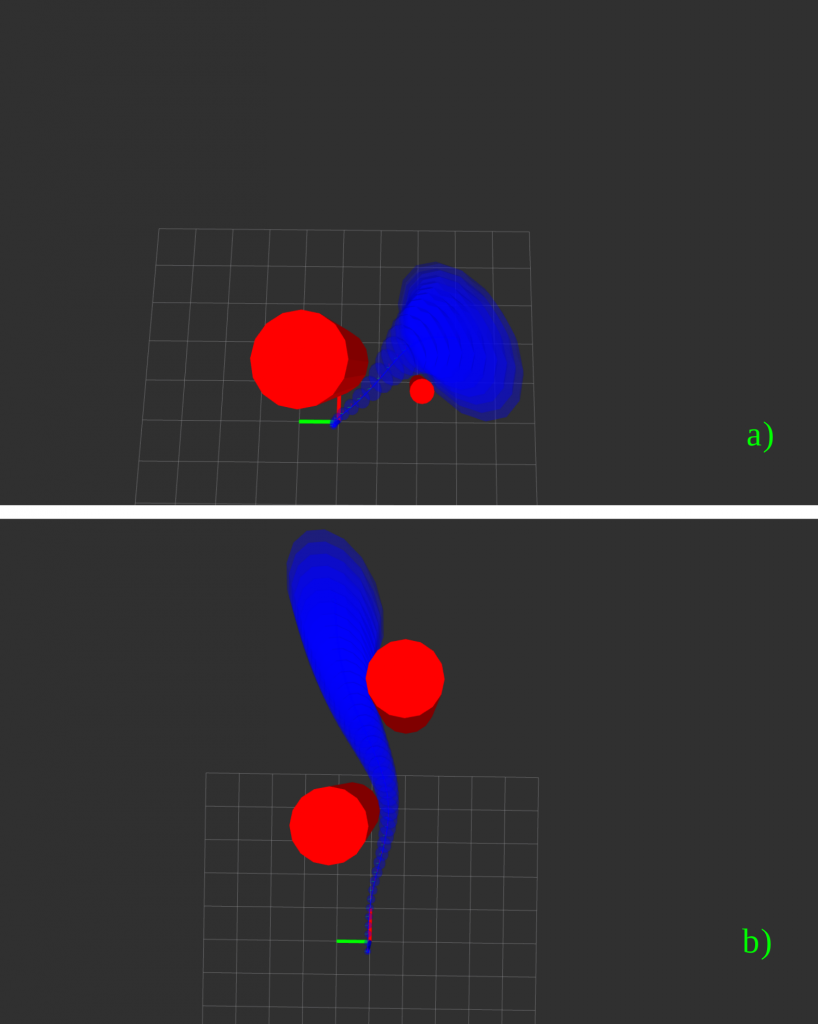
This work considers Adaptive Model Predictive Control of Quadrotor Vehicles. A nonlinear model of the quadrotor is estimated online. This model is used to plan safe trajectories around obstacles. The optimal trajectory accounts for the uncertainty in the state space, and also minimizes the control effort while achieving a goal state at the same time.

Algorithms for modeling, dynamics simulation and optimal control that respect and exploit the geometric structure of the state space. The goal is to design more physically realistic, numerically stable and efficient algorithms. The core idea is to employ a unifying variational principle over set of discrete paths for 1) deriving the dynamics and 2) computing the optimal path. The resulting algorithms preserve momentum, state space structure, and exhibit stable energy behavior. This allows coarser discretization without singularities and thus improved computational efficiency for integration and optimization purposes.

Optimal estimation of the state of a dynamic observable using a mobile sensor. The main goal is to compute a sensor trajectory which minimizes the estimation error over a given time horizon taking into account the uncertainty in the observable dynamics and its sensing and respecting the constraints of the workspace. The main contribution is a methodology for handling arbitrary dynamics, noise models and environment constraints in a global optimization framework. It is based on sequential Monte Carlo methods and sampling-based motion planning. Three variance reduction techniques–utility sampling, shuffling, and pruning–based on importance sampling, are proposed to speed-up convergence. The developed framework is applied to two typical scenarios: a simple vehicle operating in a planar polygonal obstacle environment; a simulated helicopter searching for a moving target in a 3-D terrain.